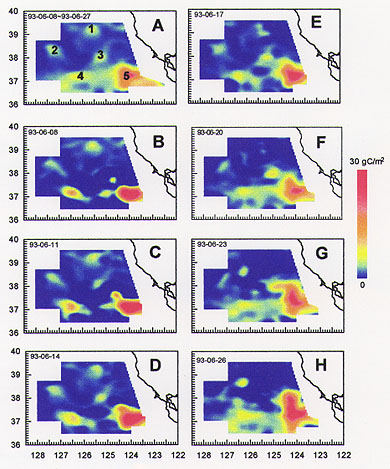
Figure 1. Zooplankton distribution. (A) the direct interpolation of OPC samples, and (B)-(H) the Lagrangian-Eulerian objective interpolation at 0 hour on the given day indicated on the upper-left corner of each panel.
Our objective is to understand how spatial and temporal variability in mesoscale circulation constitutes the dominant physical forcing on zooplankton biomass, production and distribution in the California Current system. We have taken an approach first to use models for the study of individual physical and biological processes, and then to couple these processes spatially and temporally by using a 3-d circulation-ecosystem model. The processes that drive changes in zooplankton distribution are advection and population dynamics. We developed a statistical Lagrangian model for the time evolution of zooplankton distribution in a flow field [Zhou, 1998]. The result shows that the zooplankton distribution in the California Current system is very transient (Figures 1 and 2). The zooplankton maximums associated convergent eddies have longer residence time than those in current jets. As the California Current sweeps inshore zooplankton population offshore and southward, the nearshore counter current advects zooplankton population from the south to the north.

Figure 1. Zooplankton distribution. (A) the direct interpolation of OPC samples, and (B)-(H) the Lagrangian-Eulerian objective interpolation at 0 hour on the given day indicated on the upper-left corner of each panel.
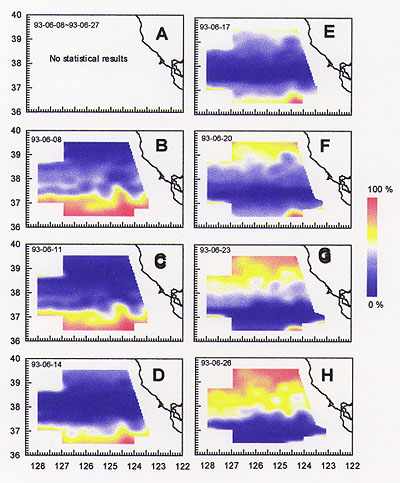
Figure 2. Relative errors of OPC data at 95% confidence level. (A) no statistical results, and (B)-(H) the objective error mapping at 0 time on the day indicated in the upper-left corner of each panel.
To verify our population dynamics model and estimates of individual and population growth rates, we took the advantage of having the 2-year time series of size-structured zooplankton population measured at JGOFS-HOTS Station. The results demonstrated our model is accurate and robust (Figure 3).
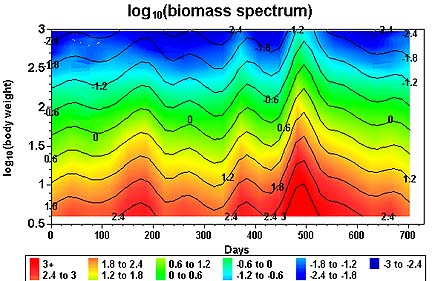
Figure 3. Biomass spectra from both modeling (contours) and observations (color) at JGOFS Hot Station. The first day starts from Feb. 4, 1995.
References
Fasham, M.J.R., H.W. Ducklow, and S.M. McKelvie, A nitrogen-based model of plankton dynamics in the oceanic mixed layer, Journal of Marine Research, 48, 591-639, 1990.
Huntley, M., and C. Boyd, Food-limited growth of marine zooplankton, American Naturalist, 124 (4), 455-478, 1984.
Pütter, A., Studien über physiologische Änlichkeit. VI. Wachstumsähnlichkeiten., Pfluegers Archiv für die Gesamte Physiologie des Menschen und der Tiere, 180, 298-317, 1920.
von Bertalanffy, L., A quantitative theory of organic growth (inquiries on growth laws. II), Human Biology, 10, 181-213, 1938.
Zhou, An Objective Interpolation Method for Zooplankton Spatiotemporal Distribution, Marine Ecology Progress Series, 174, 197-206, 1998.
Zhou, M., and M.E. Huntley, Population dynamics theory of plankton based on biomass spectra, Marine Ecology Progress Series, 159, 61-73, 1997.